Movimiento de proyectiles con resistencia lineal del aire

 Vamos a considerar el movimiento de un proyectil que esta sujeto a una fuerza de resistencia debido al aire, en este caso la energía no se va a conservar ya que esta, por acción de la fuerza de resistencia, disminuirá durante el vuelo, y también, vamos a asumir que la fuerza de resistencia varia linealmente, con lo que podemos tener una constante de proporcionalidad mℽ donde m es la masa del proyectil, y con esto tendremos una ecuación de movimiento de la siguiente manera:

y de esto podemos ver claramente que las masas se cancelan, quedando

y ya que estamos en tres dimensiones podemos ver la aceleración en cada una de las dimensiones, las cuales serán:

vamos a solucionar estas tres ecuaciones, de la siguiente manera, para la primera

y para las otras dos ecuaciones son procedimientos similares, por lo que los resultados nos quedan como

vamos a orientar nuestro sistema de coordenadas de tal modo que el eje x se encuentre a lo largo de la proyección de la velocidad inicial sobre el plano xy, por lo cual tendremos que

y esto hace que el movimiento este limitado únicamente al plano xz, vamos a integrar una vez mas las velocidades en x y z para obtener las coordenadas de posición, primero lo hacemos con el termino en x

ahora para la ecuación de z

ahora con las ecuaciones (23) y (33) podemos crear una ecuación vectorial para la posición, la cual será la siguiente, el procedimiento que hacemos es para que se pueda visualizar mejor la construcción de la ecuación vectorial,

en este caso la trayectoria no es una parábola sino mas bien una curva que se encuentra por debajo de una parábola como la descrita en el caso sin resistencia del aire, si tomamos la ecuación (23) de x y hacemos que el tiempo sea muy grande, el valor aproximado del limite será:

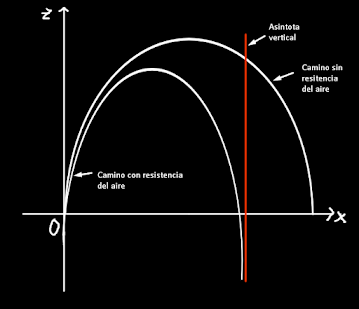Figura 2

y suponiendo que si el proyectil no golpea nada, o puede pasar el nivel de referencia del cual partió,

este tendrá una asíntota vertical y su movimiento seguirá, como en la figura 2.

<- Propiedades del movimiento de un proyectil sin resistencia del aire

Oscilador armónico isotrópico en dos dimensiones ->