Constantes de movimiento y condiciones iniciales del movimiento armónico
Comencemos partiendo de la solucion del movimiento armónico simple el cual tiene dos constantes arbitrarias A y 𝜙0
el valor de cada constante lo podemos encontrar sabiendo las condiciones iniciales, primero consieremos el caso en que el oscilador esta en la posición x = 0 al tiempo t = 0, y ambien tomamos
que la fase inicial esta dada por 𝜙0 = 0, entonces la velocidad v0 en t = 0 será
por lo que la constante A será
Ahora podemos considerar un evento general, en que la posición inicial está desplazada de x0 y
esta dada por la velocidad inicial v0, esto es
y para la velocidad
de (8) y (10 ) podemos hacer lo siguiente
sumamos (11) y (12)
elevamos al cuadrado ambas partes de la ecuación anterior
factorizamos A
A partir de esta ultima solución mas general podemos encontrar las anteriores haciendo x0 = 0 o
vo = 0.



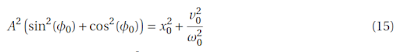



Comentarios
Publicar un comentario