Ecuaciones de movimiento con fuerzas dependientes de la velocidad - caida vertical lineal-
A menudo nos encontramos que la fuerza que actúa sobre un cuerpo esta en función de la
velocidad del mismo cuerpo, esto es, si la fuerza se puede expresar como una función solamente
de v, la ecuación de movimiento la podemos escribir de cualquiera de las siguientes dos maneras:
donde F0 es una fuerza constante que no va a depender de v, en donde explícitamente v = v(t ).
Para calcular F(v), por lo general se debe hacer a través de mediciones experimentales, sin embargo
la siguiente expresión da una aproximación buena para muchos casos
en donde c1 y c2 son valores constantes que dependen del tamaño y forma del cuerpo.
Vamos a revisar dos casos de caída vertical a través de un fluido y su velocidad terminal, en los
casos lineales y cuadráticos.
Caso lineal
Para el caso lineal la fuerza F0 es el peso del objeto, que llamamos -mg ya que tenemos la
misma consideración de ejes que en el caso de caída libre, en el eje x los valores positivos van
hacia arriba y los negativos hacia abajo, entonces nuestra ecuación de movimiento será:
si separamos las variables vamos a tener lo siguiente
ahora si a continuación integramos y resolvemos
resolviendo esta integral
para la integral del lado derecho tenemos que si
entonces
por lo cual
con lo cual tenemos finalmente que
en donde v0 es la velocidad inicial en t = 0 = t0, entonces
a continuación vamos a resolver para v,despejando de (19)
La velocidad límite a la que llega un cuerpo en caída libre es su velocidad terminal y esta pasa
cuando la velocidad del objeto y la fuerza de resistencia del fluido que atraviesa son iguales y
opuestas entre si, con lo cual la fuerza neta del sistema es 0 y entonces la aceleración también será 0. Y al igual que la velocidad y la rapidez, la magnitud de la velocidad terminal es a rapidez terminal.
Si designamos la velocidad terminal como mg /c1 y 𝛕 = m/c1, entonces la ecuación (24) será
En particular para un objeto que se deja caer desde el reposo en el tiempo t = 0 y v0 = 0, encontramos
que







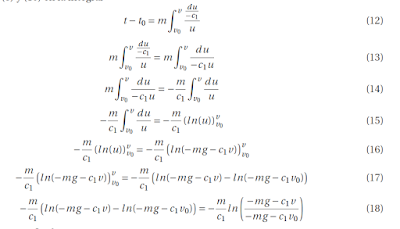






Comentarios
Publicar un comentario