Derivada del producto punto de vectores
Si tenemos dos vectores A y B los cuales están multiplicando por medio del producto escalar, tendremos la siguiente propiedad de derivadas
Probemos esto, si tenemos que los dos vectores tienen las siguientes componentes, las cuales dependen de una variable u
el producto punto entre estos dos vectores será
y si sustituimos esto en la parte izquierda de la ecuación (1) tendremos q ue la derivada del producto punto se nos convierte en lo siguiente
y esto a su vez lo podemos representar como una suma de derivadas
procedemos a realizar estas derivadas
sustituimos las derivadas de (6) en (5)
y procedemos a reagrupar los términos del lado derecho de la siguiente manera
pero si recordamos como esta definida la derivada de un vector
podemos ver que de la parte derecha de (8) en el primer paréntesis tenemos el producto punto de la derivada del vector dA/du por el vector B
y del segundo paréntesis de (8) tenemos lo siguiente
por lo cual tendremos lo siguiente
y finalmente sustituimos (12) en (8) para finalizar con la demostración de la ecuación (1).



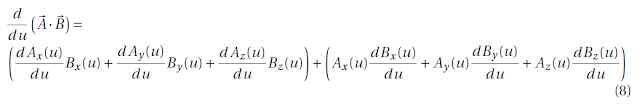






Comentarios
Publicar un comentario