Suma de vectores - propiedad conmutativa
Supongamos que tenemos dos vectores A y B, los cuales son de la misma dimensión y los culaes estan definidos como
y la suma de dos vectores esta definida como:
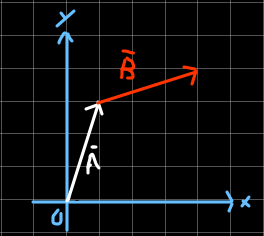
Los vectores A y B los podemos representar gráficamente de la siguiente manera
entonces tendremos que al sumar dos vectores lo que nos resultará será un nuevo vector C
pero como las componentes de ambos vectores son valores constantes, sabemos que se cumple
que
por lo que (3) lo podemos representar de la siguiente manera
y por la definición de suma de vectores vamos a tener que esto es
y tomando en cuenta (1) vemos que
pero usando (3) y (7) podemos ver lo siguiente
por lo cual vemos que la suma de vectores es conmutativa y se cumple que
esto lo podemos representar gráficamente de la siguiente manera, primero colocando el vector A
y posteriormente colocando el vector B en la punta del vector A
y para obtener la suma de los dos vectores vamos a trazar un nuevo vector que comience en el origen O y termine en donde termina el vector B
y ésta ultima figura nos representa la suma A+ B = C.
Pero también podemos comenzar con el vector B de la siguiente manera
posteriormente colocar el vector A en donde termina el vector B
y para obtener la suma de los dos vectores vamos a trazar un nuevo vector que comience en el origen O y termine en donde termina el vector A, el cual nos representará B + A = C
también para obtener el vector C podemos usar ambos casos A + B y B +A del cual obtendremos el siguiente diagrama
y para obtener la suma de los dos vectores vamos a trazar un nuevo vector que comience en el origen O y termine en donde terminan los vectores que se tocan al final.
por esta ultima figura podemos ver que realmente se cumple la ecuación (9) A+B = B+A y vemos que la suma de vectores es conmutativa.










Comentarios
Publicar un comentario