Energía en el movimiento armónico
Consideremos una partícula que esta bajo la acción de una fuerza de restauración lineal Fx= -kx y vamos a calcular el trabajo realizado por una fuerza externa Fext que mueve la partícula desde la posición de equilibrio (x=0) hasta una posición x, ahora hacemos que la fuerza externa se solamente un poco mayor que la fuerza restauradora, esto es, la fuerza externa mueve a la partícula muy lentamente, y esto lo podemos poner como
por lo que el trabajo será
si el resorte obedece la ley de Hooke, el trabajo es como si se almacenará en el resorte en forma de energía potencial W=V(x), en donde
por lo que tendremos que la fuerza de restauración la podemos escribir como
La energía total de la partícula en movimiento armónico es la suma de las energías cinética y potencial
y de esta ecuación podemos ver que la descripción de este oscilador armónico depende cuadráticamente
de la velocidad (por la energía cinética) y la posición (por la energía potencial) y vemos que la Energía total es constante si no hay otras fuerzas mas que la de restauración.
Podemos ver el movimiento de la partícula si de (7) resolvemos para la velocidad, esto es
y esto lo podemos integrar con respecto a x para obtener t en función de x recordando que
por lo que
e integrando ambos lados de la ecuación nos queda
por lo que sustituyendo la velocidad nos queda la integral
podemos hacer los siguientes cambios de variable para que seamas fácil de manejar la integral
y la integral a resolver sería
primer, para sustituir la integral hacemos que
por lo que la derivada de u con respecto a x será
sustituimos (19) en (15)
pero de (16) vemos que x es
entonces (20) nos queda como
ahora la integral que debemos solucionar será
esto lo resolvemos de la siguiente manera, ahora nuestro cambio de variable será
sustituimos (31) y (34) en (30)
y usando la siguiente relación de las funciones trigonométricas hiperbólicas
sustituimos esto en (35) y simplificamos
por lo que finalmente I nos queda
deshacemos el cambio y tenemos que de (32)
(41) lo sustituimos en (29)
y deshacemos el cambio de u
pero esto es, por propiedades del arcsinh
entonces t es
sustituimos a y b y simplificamos
en donde C es la constante de integración y podemos poner la ecuación anterior como
en donde A es la amplitud y esta la expresamos como
pero también podemos encontrar esta expresión de la amplitud directamente de (7) encontrando los puntos de inflexión donde
entonces (7) nos quedaría como
en donde el valor de x esta entre ±A para que la velocidad sea real.
También de (7) podemos ver que el valor máximo de la velocidad vmax ocurre cuando x=0, por lo que (7) lo podemos escribir como
pero podemos del lado izquierdomultiplicar por un uno, para conservar la igualdad, de la siguiente forma
y volver a multiplicar delmismo lado por otro uno y simplificamos de la siguiente manera
y hacemos lo siguiente, vamos a tomar una parte de la ecuaión y le vamos a aplicar una raiz cuadrada
y la elevaremos al cuadrado
y sustituimos (52) en (62) y finalmente nos queda
Conforme la partícula oscile, las energías cinética y potencial se irán intercambiando, la energía en x=0 será solamente energía cinética y la velocidad sera ±vmax , toda la energía será potencial en los extremos, cuando la velocidad sea 0 y x =±A.




































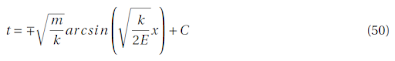









Comentarios
Publicar un comentario